तापमापी में पारा क्यों?

सुशील जोशी

सवाल बहुत आसान है, और जवाब उससे भी आसान। मगर आसान जवाबों की दिक्कत यह होती है कि यदि उसके बारे में कोई सवाल पूछ ले तो मुश्किल हो जाती है। थर्मोमीटर में पारे का उपयोग करने के बारे में पाठ्य पुस्तकों में कई बातें बताई जाती हैं। इनमें से एक यह है कि तापमान में बदलाव के साथ पारे में एकरूप फैलाव होता है। इसका मतलब यह है कि हर डिग्री तापमान बढ़ने पर पारा हमेशा उतना ही फैलता है। जैसे, यदि तापमान को 21 डिग्री से 22 डिग्री किया जाए तो जितना फैलाव होगा, उतना ही फैलाव तब भी होगा जब तापमान को 39 से 40 डिग्री या 74 से 75 डिग्री किया जाए।

वृत्ताकार तर्क का एक उदाहरण
कितना साफ-सुथरा जवाब है। मगर वही समस्या। एक जगह किसी ने पूछ लिया कि हमें कैसे मालूम कि पारे का प्रसार एकरूप है। डिग्री के निशान तो हमने ही लगाए हैं। तो हमने पारे के एक निश्चित फैलाव को इकाई मान लिया और निशान लगा दिए। जब पारे के फैलाव के आधार पर ही निशान लगे हैं तो पारा हर बार उतना ही फैलेगा, और उसी को हम एक डिग्री मानेंगे। यानी यदि हमने एक डिग्री तापमान की परिभाषा ही पारे के फैलाव के आधार पर की है, तो फिर उसी तापमापी का उपयोग करके हम पारे के प्रसार के बारे में कैसे जान सकते हैं?

मैं नहीं जानता कि यह सवाल साफ हुआ या नहीं। तर्क की भाषा में कहें तो यह वृत्ताकार तर्क (circular logic) है। खैर, इसी सवाल को दूसरे ढंग से भी पूछ सकते हैं। जब हम कहते हैं कि तापमान में 1 डिग्री की वृद्धि हुई है तो हमारा आशय क्या होता है? क्या इसका मतलब यह है कि किसी वस्तु का तापमान प्रत्येक एक डिग्री बढ़ाने पर हर बार उसमें ऊष्मा की मात्रा में बराबर वृद्धि होती है? सवाल तो यह भी है कि क्या ऊष्मा में बराबर वृद्धि होने पर वस्तु की लम्बाई-चौड़ाई में हर बार बराबर वृद्धि होगी?

पारे का उपयोग करने के पीछे तर्क यही है कि उसमें बराबर ऊष्मा बढ़ाई जाए, तो बराबर प्रसार होगा। यदि हम कहें कि ऊष्मा का मान हम ज्र् बढ़ाते हैं तो पारे के आयतन में ज्ञ् वृद्धि होती है, तो शु डिग्री का तापमान कुछ भी हो, ज्र् ऊष्मा देने पर ज्ञ् वृद्धि होनी चाहिए। समस्या यह है कि इन दो चीज़ों में से मैं तो एक ही चीज़ को नाप सकता हूँ - लम्बाई या चौड़ाई या आयतन में वृद्धि। अब मान लो मैंने किसी चीज़ को गर्म किया और वृद्धि ज्ञ् हुई, तो क्या मैं यह कह सकता हूँ कि मैंने जो ऊष्मा दी वह ज्र् थी? ऐसा कहने के लिए मुझे मानना होगा कि हर बार ज्र् ऊष्मा देने पर ज्ञ् वृद्धि होती है। क्या मेरा ऐसा मानना सही है?

तापमापी पर निशान
एक सरल उदाहरण से बात को समझते हैं। आमतौर पर तापमापी बनाते समय किया यह जाता है कि पहले काँच की बारीक नली में एक तरफ एक धातु का बल्ब लगाकर पारा भर देते हैं। अब इस नली को दोनों तरफ से बन्द कर देते हैं। बल्ब को पिघलते बर्फ में रखते हैं। पारा नली में जहाँ तक पहुँचता है, वहाँ एक निशान लगा देते हैं। फिर बल्ब को उबलते पानी में रखते हैं। पारा अधिकतम जहाँ तक पहुँचता है वहाँ दूसरा निशान लगा देते हैं। पहले निशान को शून्य और दूसरे निशान को 100 कहते हैं। अब इन दो निशानों के बीच की लम्बाई को 100 बराबर भागों में बाँटकर निशान लगा देते हैं। प्रत्येक दो निशानों के बीच की दूरी को 1 डिग्री कहते हैं।

मान लो, किसी बच्चे की लम्बाई में वृद्धि को देखना चाहते हैं। क्या करेंगे? जिस दिन बच्चा पैदा हुआ उसकी लम्बाई (ऊँचाई) नाप लेंगे। फिर 20 साल बाद उसकी ऊँचाई नाप लेंगे। इन दो के बीच की दूरी को 20 बराबर भागों में बाँट लेंगे। क्या, ऐसे जो निशान लगेंगे उसके आधार पर हम कह सकेंगे कि बच्चे की ऊँचाई प्रति वर्ष उतनी-उतनी बढ़ी है? नहीं ना? हमें करना यह होगा कि हर वर्ष बच्चे की ऊँचाई नापकर निशान लगाएँ। इसके लिए आवश्यक होगा कि हमें मालूम हो कि एक वर्ष मतलब कितना।

हम कह सकते हैं कि पहले उदाहरण में पारे की ऊँचाई में परिवर्तन बच्चे की ऊँचाई में परिवर्तन जैसा है और ऊष्मा की मात्रा वर्ष के तुल्य है। हम बच्चे की ऊँचाई भी नाप सकते हैं और वर्ष की लम्बाई भी हमें मालूम है। तो हम पता कर सकते हैं कि बच्चे की ऊँचाई में वृद्धि एकरूप है या नहीं। तापमान के मामले में हम पारे की ऊँचाई में प्रसार को तो नाप सकते हैं, मगर यह नहीं जानते कि उतना परिवर्तन कितनी ऊष्मा के कारण हुआ है क्योंकि ऊष्मा को तो हमने अलग से नापा नहीं है।
यदि यह समस्या आपकी समझ में आ गई है, तो वास्तव में, आप सत्रहवीं से लेकर उन्नीसवीं सदी तक वैज्ञानिकों के बीच चली एक प्रमुख बहस में शरीक हो गए हो।

शुरुआती तापमापी
प्रथम तापमापी का आविष्कार गैलिलियो ने किया था, ऐसा बताते हैं। वैसे इतिहास जानने वाले लोग कहते हैं कि इस मामले में गैलिलियो न तो अकेले थे, और न ही पहले। खैर, अभी नामों के पचड़े में न पड़ें। जो पहला तापमापी था, उसकी बनावट को देखते हैं। गैलिलियो या जिस किसी ने इसे बनाया हो, पहले-पहले तापमापी में एक लम्बी नली होती थी और उसके एक सिरे पर एक बड़ा बल्ब या फ्लास्क-सा होता था। इस नली को गर्म करते थे जिससे इसके अन्दर से हवा गर्म होकर निकल जाती थी। सारी हवा नहीं निकलती थी, कुछ हवा निकल जाती थी। अब गर्म अवस्था में ही इसे उल्टा करके पानी भरे एक बर्तन में खड़ा कर दिया जाता था ताकि नली का खुला सिरा पानी में डूबा रहे। जैसे-जैसे नली ठण्डी होती, पानी उसमें चढ़ जाता था और किसी एक ऊँचाई पर पहुँच जाता था। यह बन गया तापमापी, हालाँकि इसे तापदर्शी कहना ज़्यादा उचित होगा। वातावरण जब गर्म होता तो फ्लास्क और नली के अन्दर की हवा फैलती और नली में पानी की ऊँचाई कम हो जाती। जब वातावरण में ठण्डक होती तो अन्दर की हवा सिकुड़ जाती और पानी का तल ऊपर चढ़ जाता था। यह 1599 के आस-पास की बात है।

जल्दी ही अन्य वैज्ञानिकों ने इस तापदर्शी की प्रमुख समस्या पहचान ली। नली के अन्दर पानी के तल में चढ़ाव-उतार सिर्फ तापमान की वजह से नहीं आते थे। यह उपकरण एक दाबमापी यानी बैरोमीटर भी था। यदि बाहर की हवा का दाब कम हो जाए तो भी नली में पानी का तल गिर जाएगा और वायुमण्डल का दाब बढ़ जाए तो नली में पानी चढ़ जाएगा। वैज्ञानिकों को यह समझ में आ गया था कि खुली नली वाले किसी भी तापमापी में यह समस्या रहेगी, यानी ऐसे तापमापियों पर वायुमण्डल के दाब का असर पड़ता रहेगा।
उस समय तापमापियों का उपयोग मुख्य रूप से मौसम को समझने के लिए होता था। मगर धीरे-धीरे ऐसे तापमापी बनाए जाने लगे जिनसे किसी भी वस्तु का ताप नापा जा सके।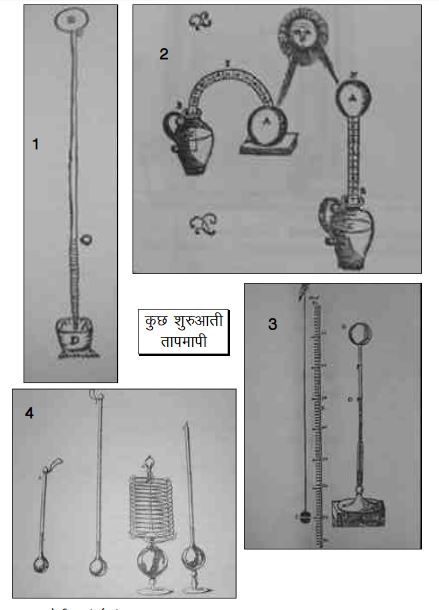
इस सम्बन्ध में एक वैज्ञानिक गिलौम एमोन्टोन्स का ज़िक्र ज़रूरी है। चिन्ता मत करो, मैं अपने मूल प्रश्न को भूला नहीं हूँ, उसी के जवाब की दिशा में बढ़ रहा हूँ।
गिलौम एमोन्टोन्स (1663-1705) फ्राँसीसी वैज्ञानिक थे और जन्म से ही बहरे थे। उनके बहरेपन और विज्ञान के सम्बन्ध की बात कभी बाद में करेंगे, यहाँ तो उनके तापमापी की बात करते हैं। उन्होंने इस बात का खूब अध्ययन किया था कि तापमान बढ़ने पर गैसों के दबाव पर क्या असर पड़ता है। इस बात को थोड़ा समझ लेते हैं। मान लो किसी बर्तन में हवा भरी है और ऊपर एक पिस्टन लगा है। पिस्टन ऐसे ढक्कन को कहते हैं जो हवा को बाहर नहीं निकलने देगा मगर खुद ऊपर-नीचे सरक सकता है। अब इस हवा को गर्म करें, तो हवा फैलेगी और पिस्टन ऊपर सरकेगा। हम करेंगे यह कि इस पिस्टन के ऊपर इतना वज़न रख देंगे कि वह सरकने न पाए। मतलब अन्दर की हवा फैल नहीं पाएगी। हवा को फैलने से रोकने के लिए हमें पिस्टन पर वज़न इसलिए रखना पड़ा है क्योंकि अन्दर की हवा पिस्टन को ऊपर धक्का दे रही है। इस धक्के को ही दबाव कहते हैं। हवा को और गर्म करेंगे तो पिस्टन को अपनी जगह रखने के लिए हमें उस पर और वज़न रखना पड़ेगा।

एमोन्टोन्स ने इसी क्रिया का अध्ययन किया यानी हवा का आयतन स्थिर रखते हुए गर्म करने पर उसके दबाव में होने वाले परिवर्तन के आँकड़े इकट्ठे किए। इन प्रयोगों के आधार पर उन्होंने एक नियम निकाला कि हवा का दबाव तापमान के साथ बढ़ता है। और इतना ही नहीं, दबाव में वृद्धि तापमान के अनुपात में होती है।
उन्होंने एक उपकरण बनाया जिसमें फ्लास्क में हवा भरने के बाद वे दूसरी ओर पारा भरते थे। फ्लास्क की तरफ की नली में पारे के तल और खुली नली में पारे के तल में अन्तर से पता चलता था कि फ्लास्क में हवा का दबाव कितना है।
तापमान नापने के लिए उन्होंने किया यह कि पहले फ्लास्क को बर्फ में रख दिया। फिर नली में पारा डालकर इसकी हवा का दबाव किसी एक मान पर ले आए। यह दबाव नापकर लिख लिया। अब फ्लास्क को उबलते पानी में रखा। थोड़ी देर बाद फिर से फ्लास्क की हवा का दबाव नापा। बर्फ के तापमान पर हवा का दबाव और उबलते पानी के ताप पर हवा के दबाव में अन्तर निकाल लिया। ध्यान देने की बात यह है कि दोनों स्थितियों में फ्लास्क में हवा का आयतन बराबर रहना चाहिए। इसके लिए नली में और पारा डालना पड़ सकता है।
तो वे जान गए कि हवा की एक निश्चित मात्रा को निश्चित आयतन में घेरकर उसका दबाव बर्फ के तापमान और उबलते पानी के तापमान पर कितना-कितना होता है। मगर यह कैसे पता चले कि क्या दबाव में यह परिवर्तन एकरूप गति से हुआ है या इसमें उतार चढ़ाव हैं?
यह जाँचने के लिए इस प्रयोग को दोहराया। मगर इस बार फ्लास्क में हवा का दबाव पहले से कुछ अलग रखा। तीसरी बार प्रयोग को दोहराते समय शुरुआती दबाव फिर कुछ और रखा। इस तरह कई शुरुआती दबावों से शु डिग्री करके उन्होंने बर्फ के ताप और उबलते पानी के ताप पर फ्लास्क की हवा के दबाव में अन्तर पता किया। इन आँकड़ों को देखने पर पता चला कि शु डिग्री का दबाव कुछ भी रखा जाए, बर्फ के ताप से उबलते पानी के ताप तक पहुँचने में दबाव में जो वृद्धि होती है वह शुरु के दबाव की लगभग 33 प्रतिशत होती है। दूसरे शब्दों में, यदि बर्फ के ताप पर शुरुआती दबाव 15 इकाई हो, तो उबलते पानी में रखने पर इसी हवा का दबाव 20 इकाई हो जाएगा। यदि हम शुरुआत 30 इकाई से करेंगे तो उबलते पानी के ताप पर दबाव 40 इकाई हो जाएगा।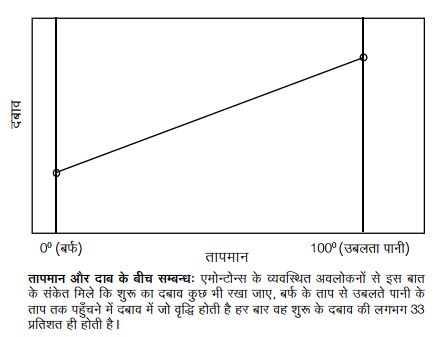

इसके आधार पर उन्होंने निष्कर्ष निकाला कि बर्फ के तापमान और उबलते पानी के तापमान पर जो दबाव हैं उनके बीच हवा का दबाव एक सरल रेखा ग्राफ के रूप में बदलता है। अर्थात् तापमान और दबाव के बीच बना ग्राफ एक सरल रेखा ग्राफ होगा। यदि आपको फ्लास्क में भरी हवा का दबाव पता है तो ग्राफ की मदद से आप उस दबाव पर हवा का तापमान पता कर सकते हैं।
एमोन्टोन्स का तर्क यही था कि किसी भी दबाव से शुरु करके गर्म करें तो दबाव में वृद्धि निश्चित होती है, इसका मतलब यही है कि यह वृद्धि एकरूप गति से होती है। अर्थात् ग्राफ पर इन दो बिन्दुओं को हम एक सरल रेखा से जोड़ सकते हैं।
यह इतना विश्वसनीय तर्क तो नहीं था मगर कामचलाऊ तो था ही। यहाँ ध्यान देने की बात यह है कि इस समय (1702-03) तक यह स्पष्ट नहीं हुआ था कि हवा एक मिश्रण है और दुनिया में कई अलग-अलग गैसें पाई जाती हैं। अभी कार्बन डाईऑक्साइड, ऑक्सीजन, नाइट्रोजन, हाइड्रोजन की खोज नहीं हुई थी। लिहाज़ा एमोन्टोन्स ने सारे प्रयोग हवा के साथ ही किए थे और उनका निष्कर्ष था कि हवा का दबाव तापमान के समानुपाती है।

फैरनहाइट तापमापी
अब तक तापमापी का महत्व सबकी समझ में आने लगा था। और यह माँग होने लगी थी कि ऐसे तापमापी होने चाहिए जिन्हें आसानी से यहाँ-वहाँ ले जाया जा सके। इसी के चलते द्रव वाले तापमापी बनाने की कोशिश हुई। सबसे पहले द्रव भरे तापमापी 1650 में बनाए गए थे। पहले अल्कोहल भरकर काम चलाया गया मगर फिर पारा भरा गया। सबसे पहले पारा भरने का विचार शायद बैरोमीटर से आया होगा मगर पारे की एक और विशेषता भी है। गर्म करें तो वह जल्दी से गर्म हो जाता है। इसलिए इसके तापमापी तुरन्त काम करते हैं।
खैर, इस समय तक ऊष्मा को नापने का एक नया तरीका आ चुका था - इसे मिश्रण विधि कहते हैं। इस विधि का उपयोग आज भी ऊष्मा सम्बन्धी प्रयोगों में किया जाता है। मान लो कि 100 ग्राम पानी है उबलते पानी के तापमान पर और 100 ग्राम पानी है बर्फ के तापमान पर। इन दोनों को मिला दिया। मिश्रण का तापमान कितना होगा? देखा गया कि इस मिश्रण का तापमान दोनों पानी के तापमान के लगभग बीच में आता है। यानी बर्फीले पानी और उबलते पानी के जो तापमान हमने अंकित किए थे, उनके लगभग बीच में इस मिश्रण का तापमान आता है। तो हमारा बीच का बिन्दु ठीक लग जाएगा। पानी में मिलावट का यह प्रयोग अलग-अलग तापमान (मगर समान मात्रा) के पानी को मिला-मिलाकर किया गया तो पता चला कि मिश्रण का तापमान उबलते पानी की मात्रा के समानुपाती होता है।

इससे एक महत्वपूर्ण निष्कर्ष निकाला जा सकता है - पानी के तापमान को 0 से 50 डिग्री तक बढ़ाने में जितनी ऊष्मा लगती है, लगभग उतनी ही ऊष्मा उसे 50 से 100 डिग्री तक ले जाने में भी लगेगी।
ऐसे कई प्रयोगों की मदद से पता चला कि 1 घन से.मी. पानी का तापमान 1 इकाई बढ़ाने के लिए हमेशा बराबर मात्रा में ऊष्मा की ज़रूरत होती है।

इसके आधार पर तापमापी पर निशान लगाने का काम ज़्यादा व्यवस्थित हो गया। फैरनहाइट ने इन प्रयोगों के आधार पर काँच की नली में पारा भरकर एक तापमापी बनाया और उस पर पैमाना भी अंकित किया। फैरनहाइट ने किसी कारण से तय किया था कि बर्फीले पानी का तापमान 32 डिग्री रखेंगे और उबलते पानी का तापमान 212 डिग्री। इनके बीच की दूरी को उन्होंने 180 बराबर भागों में बाँट दिया। प्रत्येक भाग एक डिग्री फैरनहाइट हुआ।

काँच के प्रसार का क्या करें?
अब लोग मानने लगे थे कि हाँ, पारे का प्रसार एकरूप होता है। ऐसा इसलिए कि पानी के मिश्रणों के आधार पर जो तापमान निकलते थे वे पारे के पैमाने से मेल खाते थे। लेकिन...अभी कहानी पूरी नहीं हुई।
कुछ ही वर्षों में तापमापी बड़े पैमाने पर बनने लगे थे। किसी ने जब ऐसे कई पारा तापमापियों की तुलना की तो पाया कि ये सब एक ही पानी में रखे जाने पर अलग-अलग तापमान दर्शाते हैं, जबकि इनका निर्माण काफी सावधानीपूर्वक किया गया था। अन्तर 2 डिग्री तक का था। इस समय तक सब लोग पारे के गुणों पर ध्यान दे रहे थे। अब पहली बार काँच पर ध्यान गया। पता चला कि पारे के तापमापी में कई कारणों से अन्तर आ जाते हैं।

जब हम पारे के तापमापी का उपयोग करते हैं तो पारा तो फैलता ही है, काँच भी तो फैलता है। काँच कोई शुद्ध पदार्थ नहीं है। अलग-अलग काँच का प्रसार अलग-अलग होता है। और-तो-और काँच का प्रसार उतना नियमित भी नहीं होता - पहले वह धीरे-धीरे फैलता है, बाद में जल्दी-जल्दी फैलता है।
एक दिक्कत यह भी थी कि काँच की एकरूप सुराख वाली नली बनाना भी मुश्किल था। जहाँ नली पतली होगी वहाँ पारा ज़्यादा चढ़ेगा, जहाँ नली चौड़ी होगी वहाँ धीरे-धीरे चढ़ेगा। इसका एक तरीका निकाला गया था। पारे की एक निश्चित मात्रा लेकर उसे नली में डाल देते थे। फिर नली में इसे अलग-अलग स्थानों पर ले जाकर इसकी लम्बाई नापते थे। यदि लम्बाई बराबर आए तो नली का सुराख एकरूप है।

काँच के प्रसार और पारे के प्रसार में काफी अन्तर है, इसीलिए काँच की नली में पारा चढ़ता है। यदि दोनों का प्रसार बराबर या लगभग बराबर होता तो शायद पारा न चढ़ता। मगर इन दोनों के प्रसार में अन्तर उतना ज़्यादा भी नहीं है।
एक बार फिर सवाल उठने लगे कि पारे का उपयोग उचित है या नहीं। मतलब एक बार फिर पूछा जाने लगा कि पारे का प्रसार एकरूप माना जाए या नहीं।

अब आया वायु तापमापी
इस बार जाँच का एक नया तरीका सामने आया। गौर करने की बात है कि इस समय तक हवा के मिश्रण होने की बात उजागर हो चुकी थी। कार्बन डाईऑक्साइड व ऑक्सीजन गैसें बनाई जा चुकी थीं। तो रेनो नामक वैज्ञानिक ने इन अलग-अलग गैसों से एमोन्टोन्स टाइप के तापमापी बनाए और इनकी आपस में तुलना की। उन्होंने पाया कि सबके सब एक जैसे परिणाम देते हैं। प्रयोग इस तरह किया जाता था - दो वायु-तापमापी हैं। एक में हवा भरी है, दूसरे में कार्बन डाईऑक्साइड। दोनों के फ्लास्क को एक ही पानी में पास-पास रखा गया है। अब पानी को धीरे-धीरे गर्म करते हैं और दोनों तापमापियों में गैस के दबाव के आधार पर तापमान नापते हैं। पता चला कि दोनों में पानी के गर्म होने के साथ-साथ दबाव में एक-सा परिवर्तन आता है।

इस तुलना विधि के आधार पर रेनो का निष्कर्ष था कि तापमान के साथ गैसों के दबाव में परिवर्तन एकरूप होता है। एकरूप कैसे कहा उन्होंने? यदि दो या तीन गैसों में दबाव परिवर्तन एक-सा हो रहा है तो दो ही बातें हो सकती हैं। या तो उनमें दबाव के परिवर्तन में जो चढ़ाव-उतार हो रहे हैं वे एक जैसे हो रहे हैं या फिर उतार-चढ़ाव नहीं हो रहे हैं। यह तो बहुत मुश्किल है कि दो पदार्थों में जो परिवर्तन हो रहे हैं वे ऊबड़-खाबड़ हैं मगर उनका ऊबड़-खाबड़ पन हूबहू एक समान है। तो ज़्यादा सही यही लगता है कि दोनों में हो रहे परिवर्तन एकरूप हैं।

रेनो इस निष्कर्ष पर पहुँचे कि तापमापी हो, तो वायु तापमापी। पारे का तापमापी नहीं चलेगा क्योंकि उनमें आपस में बहुत अन्तर हैं। रेनो का यह भी कहना था कि गैसों के मामले में फायदा यह है कि उनके आयतन में परिवर्तन बहुत अधिक होता है, काँच की अपेक्षा बहुत ही अधिक। इसलिए काँच में अन्तरों का गैस तापमापी पर कोई असर नहीं पड़ेगा।

तो फिर हम पारे के तापमापी में कैसे उलझ गए? यह तो तय था कि गैस तापमापी सबसे सही तापमान बताते हैं। मगर इनका उपयोग करना काफी कठिन था। प्रयोगशाला में तो ठीक है मगर बुखार नापना हो, तो? इसलिए एक बार फिर तुलनाएँ की गईं। पता चला कि वायु तापमापी से तुलना करने पर पारा तापमापी उन्नीस-बीस ही ठहरता है। और यह उपयोग में सरल बहुत था। तो पारे को स्वीकार कर लिया गया। इसी दौरान अल्कोहल का उपयोग भी जारी रहा।

कुल मिलाकर बात यह है कि पारे के प्रसार का एकरूप होना पूरी तरह सिर्फ मानने की बात नहीं है। इसके पीछे कुछ ठोस प्रमाण हैं। मगर पूरी तरह एकरूप न होने पर भी यह हमारे कामकाज के हिसाब से ठीक ही है। इसलिए जहाँ एकदम सटीक व सही तापमान नापने की ज़रूरत होती है वहाँ अन्य तापमापियों का उपयोग किया जाता है। आजकल तापमापी सिर्फ प्रसार के गुण के आधार पर नहीं बनते। पदार्थों के कई गुण हैं जो तापमान के साथ बदलते हैं। उनमें से कई का उपयोग तापमापी बनाने में किया जाता है।

सुशील जोशी: एकलव्य द्वारा संचालित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान शिक्षण व लेखन में गहरी रुचि।