कम-से-कम या ज़्यादा-से-ज़्यादा

विवेक मेहता

कहा जाता है कि एक गिरते सेब को  देखकर  न्यूटन  को गुरुत्वाकर्षण का सिद्धान्त खोजने की प्रेरणा मिली थी। अगर ये बात सच है तो हो सकता है कि ऊपर की ओर उछाली गई एक गेंद या सेब की गति को देखकर उन्होंने यह बात लिखी हो -  
‘कोई राशि (quantity) जब सबसे बड़ी या छोटी होती है तो वो न आगे की तरफ बह रही होती है न पीछे। क्योंकि अगर वो आगे की तरफ बह रही होगी या ये कहें कि बढ़ रही होगी तो अपने वर्तमान मान से और ज़्यादा बड़ी हो सकती है और अगर पीछे की तरफ बह रही होगी या घट रही होगी तो अपने वर्तमान मान से और कम।’

आईए, न्यूटन के द्वारा लिखे गए इस नियम को एक ऊपर उछाली हुई गेंद की गति के सन्दर्भ में समझने की कोशिश करते हैं। उसके बाद कुछ अन्य उदाहरणों में हम न्यूटन के इस नियम  का  इस्तेमाल  कर  इसकी उपयोगिता व सीमाओं को जाँचेंगे।

उछाली गई एक गेंद की गति 
अगर एक गेंद एक शुरुआती ऊँचाई से किसी शुरुआती गति से ऊपर की ओर उछाली जाए तो कुछ देर तक ऊपर जाने के बाद वह नीचे की तरफ आने लगती है।¹ उदाहरण के तौर पर चित्र-1 में दिखाए अनुसार एक गेंद h_o मीटर की शुरुआती ऊँचाई से v_o मीटर प्रति सेकण्ड (m/s) की शुरुआती रफ्तार से ऊछाली गई है। अब यह सवाल बनता है कि नीचे आना शुरू करने से पहले गेंद अधिकतम किस ऊँचाई, h_mix मीटर तक जाएगी?

अपने अनुभव से हम जानते हैं कि गेंद की अधिकतम ऊँचाई सीधे तौर पर h_o व v_o पर निर्भर करती है।² दो अलग-अलग शुरुआती ऊँचाइयों से समान शुरुआती रफ्तार से उछाली गई दो गेंदों में से वो गेंद ज़्यादा ऊपर जाएगी जिसकी शुरुआती ऊँचाई ज़्यादा हो। इसी तरह एक ही शुरुआती ऊँचाई से दो अलग-अलग शुरुआती रफ्तारों से उछाली गई गेंदों में से वो गेंद ज़्यादा ऊपर जाएगी जिसकी शुरुआती रफ्तार ज़्यादा हो। लेकिन यहाँ सवाल ऐसी दो या चार स्थितियों में गेंद के द्वारा हासिल की गई अधिकतम ऊँचाई की तुलना का नहीं है। यहाँ सवाल है कि अगर गेंद की शुरुआती ऊँचाई h_o और शुरुआती रफ्तार v_o हो तो गेंद की अधिकतम ऊँचाई क्या होगी?

चूँकि यहाँ बात अधिकतम ऊँचाई की हो रही है तो हम न्यूटन के उस कथन का रुख करते हैं जिसमें वो किसी राशि के सबसे बड़े (या छोटे) होने की बात कह रहे हैं। न्यूटन लिखते हैं कि ‘जब कोई राशि सबसे बड़ी होती है तो वो न आगे की तरफ बह रही होती है न पीछे’। इस उदाहरण में हम जिस राशि के अधिकतम मान की बात कर रहे हैं, वो है गेंद की ऊँचाई h। अगर हम गेंद के ऊपर की ओर जाने को आगे और नीचे की ओर आने को पीछे मान लें तो इस सन्दर्भ में न्यूटन के कथन के मायने हुए कि जब गेंद अपनी अधिकतम ऊँचाई पर होगी तो वो न ऊपर की तरफ बढ़ रही होगी, न नीचे की ओर। जिसका मतलब हुआ कि ठीक उस क्षण जब गेंद अपनी अधिकतम ऊँचाई पर होगी तो वो रुकी हुई होगी यानी कि उसकी रफ्तार शून्य होगी।

इस बात को हम एक ग्राफ की मदद से भी समझ सकते हैं। गति के नियमों से हम जानते हैं कि समय के किसी भी मान t के लिए गेंद की ऊँचाई होगी;
                h = h_o + v_ot + (1/2)at²   (E-1)
गेंद पर लगातार गुरुत्वाकर्षण का बल लग रहा है जोकि उसे नीचे ग्राउंड की तरफ खींच रहा है जिस वजह से त्वरण a = –g = –9.81m/s² होगा। अगर हम  h_o = 1m  व  v_o= 5m/s लेकर समीकरण (क-1) के लिए ऊँचाई-समय का ग्राफ बनाएँ तो वो चित्र-2 की तरह होगा।

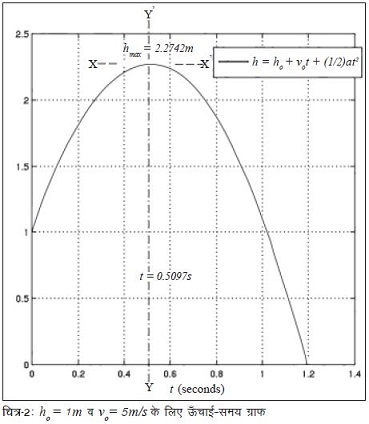हम ग्राफ में देख सकते हैं कि समय बढ़ने के साथ-साथ किस तरह गेंद पहले ऊपर की ओर जाती है और फिर t = 0.5097s पर अपनी अधिकतम ऊँचाई h_max = 2.2742m हासिल करने के बाद नीचे की ओर गिरने लगती है। अब न्यूटन साहब के कहे मुताबिक गेंद की रफ्तार अधिकतम ऊँचाई पर शून्य होनी चाहिए। एक दूरी-समय ग्राफ पर खींची गई एक स्पर्श-रेखा की ढलान उस समय-विशेष के लिए वस्तु की रफ्तार को दर्शाती है। क्या आप चित्र-2 में दिखलाए गए ग्राफ पर वो बिन्दु ढूँढ़ सकते हैं जिस पर खींची गई स्पर्श-रेखा की ढलान शून्य हो? आप देखेंगे कि t = 0.5097s के लिए ग्राफ पर जो बिन्दु है, यानी कि अधिकतम ऊँचाई वाला बिन्दु, उस पर खींची गई स्पर्श रेखा XX’ की ढलान शून्य है क्योंकि यह समय-अक्ष के समानान्तर है।

बिना ग्राफ की मदद के भी हम एक से ज़्यादा तरीकों से ये समय निकाल सकते हैं। गति के दूसरे नियम से हम जानते हैं कि समय के किसी भी मान t के लिए गेंद की रफ्तार होगी,

v = v_o + at         (E-2)

समीकरण (E-1) से dh/dt निकालने पर भी हमें समीकरण (E-2) ही मिलता। समीकरण (E-2) को शून्य के बराबर रखकर हम t का वह मान निकाल सकते हैं जब v = 0 हो। इस तरह मिले t के मान को समीकरण (E-1) में रखकर हम अधिकतम ऊँचाई भी निकाल सकते हैं। करके देखिए।

इस उदाहरण में हमने देखा कि कैसे न्यूटन के सुझाए नियम की मदद से हम एक शुरुआती ऊँचाई से किसी शुरुआती गति से ऊपर की ओर उछाली एक गेंद के द्वारा हासिल की गई अधिकतम ऊँचाई निकाल सकते हैं।

क्या चींटियाँ भी जानती हैं न्यूटन का नियम?
एक के पीछे एक लगी चींटियों को खाने की किसी चीज़ को उठाकर अपनी बांबी में ले जाते तो आप सभी ने देखा होगा। अगर नहीं देखा तो आगे सुझाया हुआ प्रयोग करके देखिए। अपने घर, बगीचे, खेल के मैदान या और कहीं भी जहाँ आपको कुछ चींटियाँ व उनकी बांबी दिखाई दें तो वहीं कुछ दूरी पर खाने की कोई चीज़ रख दीजिए।  आप  पाएँगे  कि  अमूमन चींटियाँ अपनी बांबी और खाने की जगह के बीच उपलब्ध सबसे छोटा रास्ता खोज लेती हैं। क्या वे भी न्यूटन का नियम जानती हैं?

विवेक मेहता: आई.आई.टी., कानपुर से मेकेनिकल इंजीनियरिंग में पीएच.डी. की है एवं तेज़पुर विश्वविद्यालय, असम में पढ़ा रहे हैं।